A DAX expression usually does not require a cast operation to convert one data type into another. You can use a string in a numeric expression and the string is automatically converted into a corresponding number, as long as the string is a valid representation of a number. The same automatic conversion takes place between different numeric data types. In this case, the result of the expression might not be obvious; indeed, the differences in the rounding of decimals between different data types might cause different results, depending on the data type of the operands and on the operators used in the expression.
In order to understand this behavior, it is necessary to recap what the numeric data types available in DAX are. Only later will we see how the data type conversion rules affect the result.
Numeric data types in DAX
DAX offers three different numeric data types, which have an internal name that does not always correspond to the name provided in the user interface. DAX is currently used by three different products: Power Pivot, Analysis Services, and Power BI. Each of these products use different names for certain data types. In order to provide a clear distinction between these data types, in our articles and books we use the following names:
- Integer
- Decimal
- Currency
The following sections provide a description of these data types, including all the possible aliases that can be found in documentation, user interface, and DAX functions arguments.
Integer
DAX only has one Integer data type that can store a 64-bit value. All the internal calculations between integer values in DAX also use a 64-bit value. This data type is called Whole Number in the user interface of all the products using DAX. The DATATABLE function uses INTEGER to define a column of this data type.
Decimal
A decimal number is always stored as a double-precision floating point value. Do not confuse this DAX data type with the decimal and numeric data type of Transact-SQL. The corresponding data type of a DAX decimal number in SQL is Float. In the user interface of all the products using DAX, this data type is called Decimal Number. The DATATABLE function uses DOUBLE to define a column of this data type.
Currency
The Currency data type, also known as Fixed Decimal Number in Power BI, stores a fixed decimal number. It can represent four decimal points and it is internally stored as a 64-bit integer value divided by 10,000. Adding or subtracting Currency data types always ignores decimals beyond the fourth decimal point, whereas multiplications and divisions produce a floating-point value – thus increasing the precision of the result. In general, if we need more accuracy than the four digits provided, we must use a Decimal data type.
Clarifying different names for the same data types
If you find that there is a confusion between different names for the same data type, you are not alone. The reason why the Currency data type name was changed to Fixed Decimal Number in Power BI was to avoid confusion with the Currency format. A good idea in theory, but not a good practice to have different names in different products using the same language. Thus, we think it is a good idea to recap the available data types in the following table.
| SQLBI name | Power Pivot | Analysis Services | Power BI | DATATABLE arguments |
| Integer | Whole Number | Whole Number | Whole Number | INTEGER |
| Decimal | Decimal | Decimal | Decimal | DOUBLE |
| Currency | Currency | Currency | Fixed Decimal Number | CURRENCY |
Now that we have clarified the names, we are ready to discover how data type conversion works.
Data type results from arithmetical operators
Any DAX formula involving arithmetical operators ( + – * / ) might produce a result in a different data type. While this is obvious when you have different data types in the arguments, it could be less intuitive when the arguments have the same data type. Indeed, the result might have a different data type. This is important. Indeed, in a complex expression there could be many operators, but every operator defines a single expression that produces a new data type – that is the argument of the next operator. We will start looking at the resulting data type of the standard operators, showing a few examples later of how they could affect the result in a more complex expression.
NOTE: each of the following tables represents the resulting data type of an operator, where the row header represents the left operand and the column header represents the right operand.
There are no differences between addition (+) and subtraction (-) operators. When a decimal is involved, the result is decimal. Otherwise, when a currency is involved then the result is currency. The result is integer only when both operands are also integers.
| + Addition | Integer | Decimal | Currency |
| Integer | Integer | Decimal | Currency |
| Decimal | Decimal | Decimal | Decimal |
| Currency | Currency | Decimal | Currency |
| – Subtraction | Integer | Decimal | Currency |
| Integer | Integer | Decimal | Currency |
| Decimal | Decimal | Decimal | Decimal |
| Currency | Currency | Decimal | Currency |
The product (*) operator returns an integer when two integers are involved, and it returns a currency when a currency and a non-currency type are involved. In all the other cases, the result is always a decimal. The only particular case is that when multiplying two numbers of currency data type, the result is a decimal. This is reasonable even if not completely intuitive: for example, a currency exchange rate a decimal is required but a currency is expected as a result.
| * Product | Integer | Decimal | Currency |
| Integer | Integer | Decimal | Currency |
| Decimal | Decimal | Decimal | Currency |
| Currency | Currency | Currency | Decimal |
The division (/) operator displays the same behavior as the DIVIDE function. The result is always decimal, unless a currency is divided by an integer or by a decimal; in this case, the result is currency. What is not clear here is why dividing a currency by a currency returns a decimal as a result, whereas the result is still a currency in the other two cases. It would be more intuitive if all the results were decimal, or at least currency. This can generate some confusion, as we will see in the next section.
| DIVIDE / Division |
Integer | Decimal | Currency |
| Integer | Decimal | Decimal | Decimal |
| Decimal | Decimal | Decimal | Decimal |
| Currency | Currency | Currency | Decimal |
Differences in calculation because of numeric data type conversion
In order to show the differences in the calculation we can create a calculated table that can be easily inspected in Power BI to check the resulting data type and the different results in particular cases.
We start with a simple example that shows a difference in the result by changing the order of multiplications involving an integer, a decimal, and a currency. The first three variables also show how to declare a constant value of a specific data type in DAX (see comments in the code).
OrderOfMultiplications =
VAR Quantity = 100000 -- Integer
VAR Discount = 0.10 -- Decimal
VAR UnitPrice = CURRENCY ( 12.3456 ) -- Currency
VAR Result1 = UnitPrice * ( 1 - Discount ) * Quantity
VAR Result2 = Quantity * UnitPrice * ( 1 - Discount )
RETURN
ROW (
"Result1", Result1,
"Result2", Result2
)
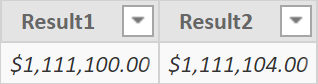
There is a difference between Result1 and Result2, caused by the order of the multiplications. If the discount is applied to UnitPrice before multiplying it by Quantity, then the quantity will multiply a currency data type that only has 4 digits after the decimal point. By changing the order of the operands in the two multiplications, the rounding to a currency data type occurs at a different stage. Depending on business requirements, one of the two versions should be the correct one and the DAX code should just implement the expected version – which is not necessarily Result2.
The second example tests the different data types of a division involving the currency data type. This is just an educational exercise to get acquainted with the different data types, showing that small differences in the decimal part might produce side effects in expressions that follow.
StudyDivisions =
VAR A =
CURRENCY ( 2 ) / 3
VAR B =
CURRENCY ( 2 ) / CURRENCY ( 3 )
VAR C =
CURRENCY ( 2 ) / 3.0
VAR A_B = ( A - B ) * 100000
VAR A_C = ( A - C ) * 100000
VAR B_C = ( B - C ) * 100000
RETURN
ROW (
"A", A,
"B", B,
"C", C,
"A-B", A_B,
"A-C", A_C,
"B-C", B_C
)

The division of a currency only returns a decimal when the denominator is another currency (B), otherwise the result is always a decimal (A and C). Computing the differences of these results is an artificial way to highlight how these differences might propagate in a more complex calculation. However, a better example is required to clarify the possible side effects of these small differences.
The third and last example computes an estimate, based on the average price computed using an amount stored in a currency or decimal data type. Although the starting number is identical, the calculation of the average price generates a decimal or a currency depending on the data type of the initial amount. This results in a difference that is propagated in the result.
EstimateSample =
VAR AmountDecimal = 10000000.0
VAR AmountCurrency = CURRENCY ( 10000000 )
VAR Quantity = 3000000
VAR Forecast = 20000000
VAR AveragePriceDecimal = AmountDecimal / Quantity
VAR AveragePriceCurrency = AmountCurrency / Quantity
VAR EstimateDecimal = AveragePriceDecimal * Forecast
VAR EstimateCurrency = AveragePriceCurrency * Forecast
RETURN
ROW (
"EstimateDecimal", EstimateDecimal,
"EstimateCurrency", EstimateCurrency
)

The difference produced by this last example is very noticeable; it is only partially mitigated by the name of the result (estimate). However, you might be unable to justify these differences with the report name, so be prepared to evaluate how to correctly implement the desired result.
Conclusions
When an expression includes multiplications and divisions between operands of different data types, it is important to consider whether the currency data type is involved. The order of the calculation for the multiplications and the presence of a currency in the numerator of a division might produce different results because of the point in the calculation where the conversion is made. The currency data type is important to avoid certain rounding errors in aggregations, but it should be managed carefully to avoid other types of rounding errors in complex expressions.
Returns a table with data defined inline.
DATATABLE ( <name>, <type> [, <name>, <type> [, … ] ], <data> )
Returns the value as a currency data type.
CURRENCY ( <Value> )
Safe Divide function with ability to handle divide by zero case.
DIVIDE ( <Numerator>, <Denominator> [, <AlternateResult>] )
 Marco Russo
Marco Russo