The VertiPaq engine is basically data type-independent. This means that it does not matter whether a column is a string, a floating point, or a date: because of the dictionary encoding happening inside VertiPaq, all these data types use around the same amount of memory and perform at nearly the same speed.
However, when mixing different data types in the same expression, DAX will likely need to perform conversions between data types. Some of these conversions are nearly free, whereas others require the intervention of the formula engine, with a related performance impact.
We have already written about possible errors occurring during data type conversion here: Understanding numeric data type conversions in DAX and here: Rounding errors with different data types in DAX. The issue with conversion errors is mostly due to the fact that the precisions of fixed decimals (also known as Currency) and decimals (also known as floating point) are different. This article starts with a focus on performance.
Performance impact of data type conversion
Data type conversion is a delicate topic. Due to the nature of computers, a real number cannot be represented in full detail. Computers always store an approximation of the real number by limiting the number of digits available. In nearly all scenarios, this is not an issue. For example, a Decimal number is a floating point that uses 15 significant digits, which is mostly overkill for any semantic model. When converting one data type to another, extra care must be taken to ensure that the conversion introduces the smallest error possible. An error is pretty much always present. However, if it is small enough, it does not really matter. Most developers simply trust their formula to produce correct numbers, even though there are rounding errors nearly everywhere, in any calculation performed by a computer. Most results are wrong, but they are wrong at a level of detail that people will never notice. Hence, we consider them to be correct.
With all that said, whenever mathematical operations happen, Power BI needs to ensure that the error introduced is small and consistent; that is, if an error occurs, it must always be the same. To achieve this goal, the code for some operations is centralized in the formula engine. In certain scenarios, a simple multiplication requires a callback from the storage engine to the formula engine, negatively affecting performance.
We are going to analyze currency conversion in the Contoso sample database as an example. Sales transactions are stored in USD. Each transaction stores both the original currency code and the conversion rate used to generate the USD value.
Here are the tables used for this example.
We want to produce a report that shows both the value in USD and the original currency. It seems like a smart idea to store the conversion rate directly in the Sales table to avoid – at query time – the conversion rate lookup on the transaction date. Hence, we store the conversion rate in the Sales[Exchange Rate] column. Because the conversion rate requires a large precision, we used a Decimal data type to avoid using only four decimal digits. Then, we create a simple measure:
Original Amount =
SUMX (
Sales,
Sales[Exchange Rate] * Sales[Quantity] * Sales[Net Price]
)
Despite looking innocent, this measure can be very expensive to compute. Sales[Quantity] is an integer, Sales[Net Price] is a fixed decimal, Sales[Exchange Rate] is a decimal. Performing the multiplication requires the intervention of the formula engine because the storage engine cannot complete the multiplication of a decimal by a fixed decimal. Let us see the behavior with a test query:
EVALUATE
ADDCOLUMNS (
SUMMARIZE (
Sales,
'Currency'[Currency Code]
),
"Original Amount", [Original Amount],
"USD Amount", [Sales Amount]
)
The result is correct: it reports the values in the original currency and in USD.
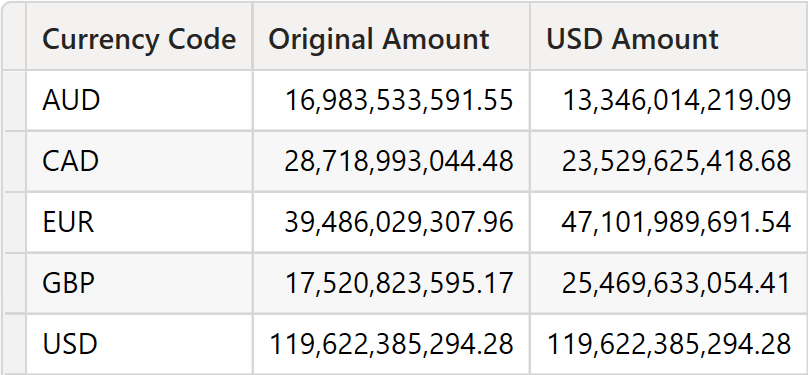
However, looking at the server timings, we are in for a nasty surprise.
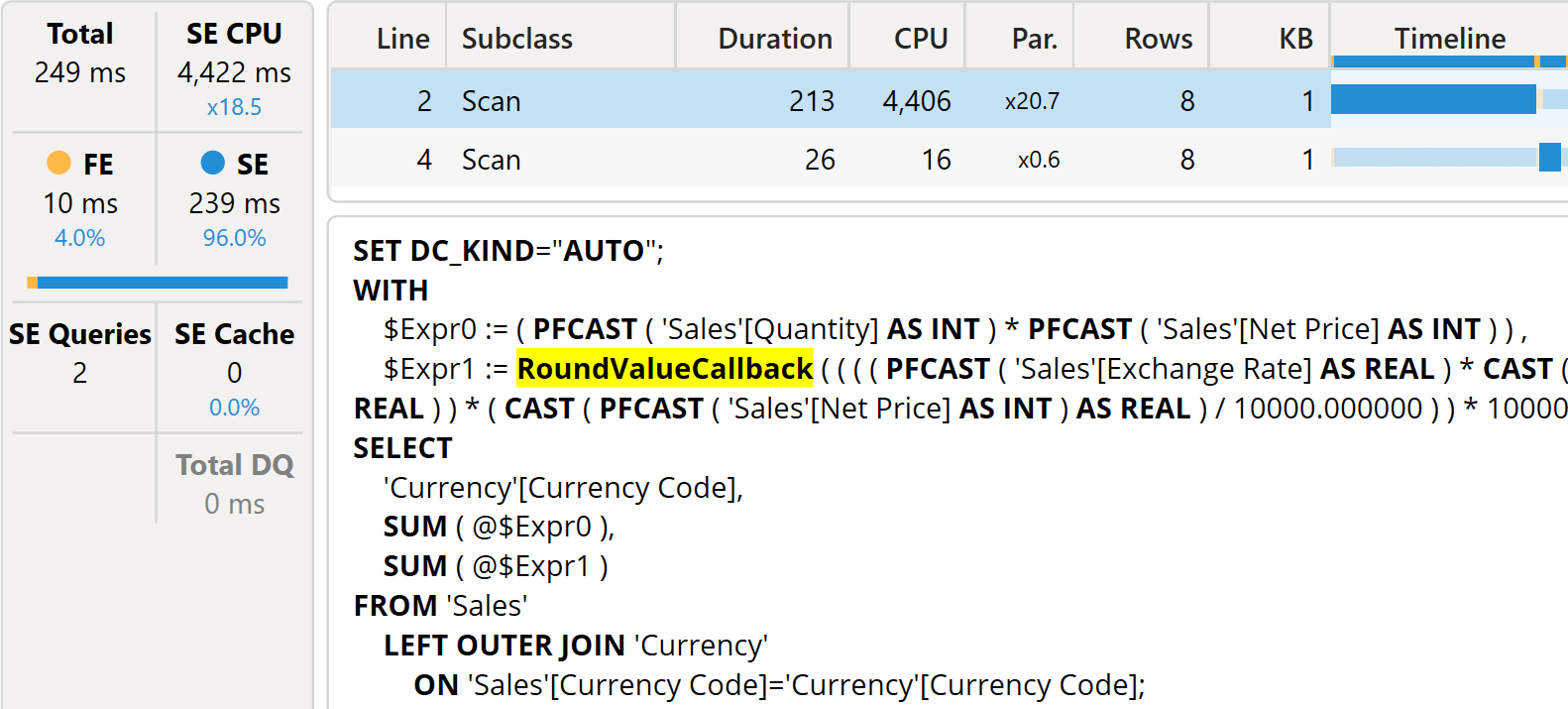
The first storage engine query includes a callback, a RoundValueCallback, which is a request for a callback to the formula engine to perform a calculation that requires rounding.
Despite running quite fast (on our 225M rows model it runs in 249 milliseconds), we notice that the speed is due to the massive amount of parallelism. The total cost of the storage engine CPU (SE CPU) is more than four seconds (4,422 ms). Hence, the speed is not due to the algorithm being good: the speed is only achieved thanks to the large number of cores available.
A simple multiplication involving decimals and fixed decimals is already over the storage engine’s head. The problem is that multiplications must be executed by the formula engine. Therefore, the callback requires a lot of time, as it is invoked 225M times.
A naive option to make the code faster is to change the data type of Sales[Exchange Rate]. Making it a Fixed Decimal would make the code faster. The error introduced may be either too large or acceptable depending on the precision needed for the calculation. Here is a query to test the error:
DEFINE
MEASURE Sales[Original Amount] =
SUMX (
Sales,
Sales[Exchange Rate] * Sales[Quantity] * Sales[Net Price]
)
MEASURE Sales[Original Amount Currency] =
SUMX (
Sales,
CURRENCY ( Sales[Exchange Rate] ) * Sales[Quantity] * Sales[Net Price]
)
EVALUATE
ADDCOLUMNS (
SUMMARIZE (
Sales,
'Currency'[Currency Code]
),
"Original Amount", [Original Amount],
"Original Amount Currency", [Original Amount Currency]
)
As you see, the numbers are different.
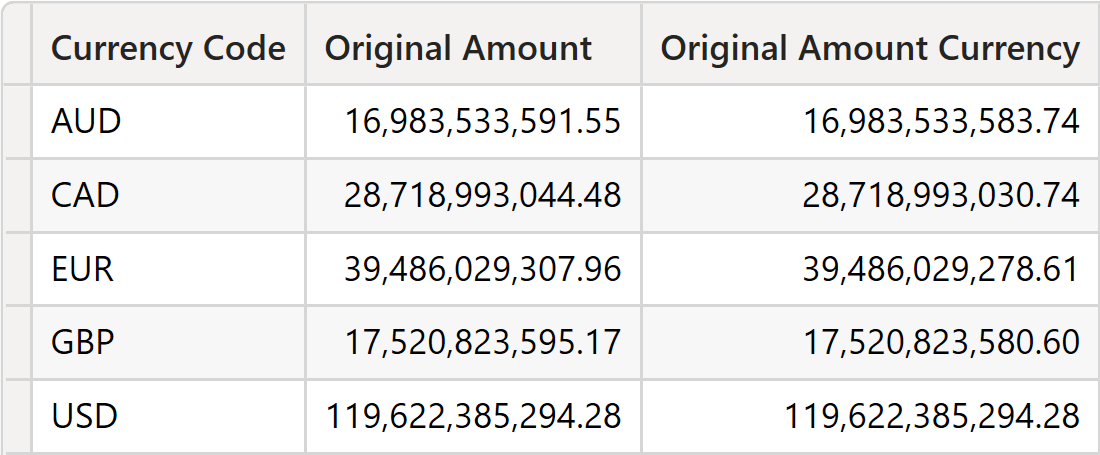
Whether the error introduced is acceptable or not depends on the specifics of the business. Be mindful that – despite seeming like the wrong solution – in this specific case, it could be just fine. As you will see later, errors are always there; you only need to decide on the error level you will tolerate. The error introduced by performing the conversion row-by-row is acceptable in this case. Generally speaking, reducing the precision of a value at the individual transaction level is not the best option because the error is introduced very early in the calculation process, and then it is propagated further through multiplications and sums in the final measure.
A better option is to reduce the number of multiplications. Indeed, because of how the formula is written, instead of iterating over each row of Sales, the measure could iterate over the distinct values of the exchange rate, perform the multiplication, and then aggregate the results through a SUMX iteration:
Original Amount =
SUMX (
VALUES ( Sales[Exchange Rate] ),
Sales[Exchange Rate] * [Sales Amount]
)
This second version of the code iterates the distinct values of Sales[Exchange Rate]. Hence, the storage engine will produce the sales amount grouped by Sales[Exchange Rate], demanding that the formula engine perform the multiplication. This is evident by looking at the server timings.
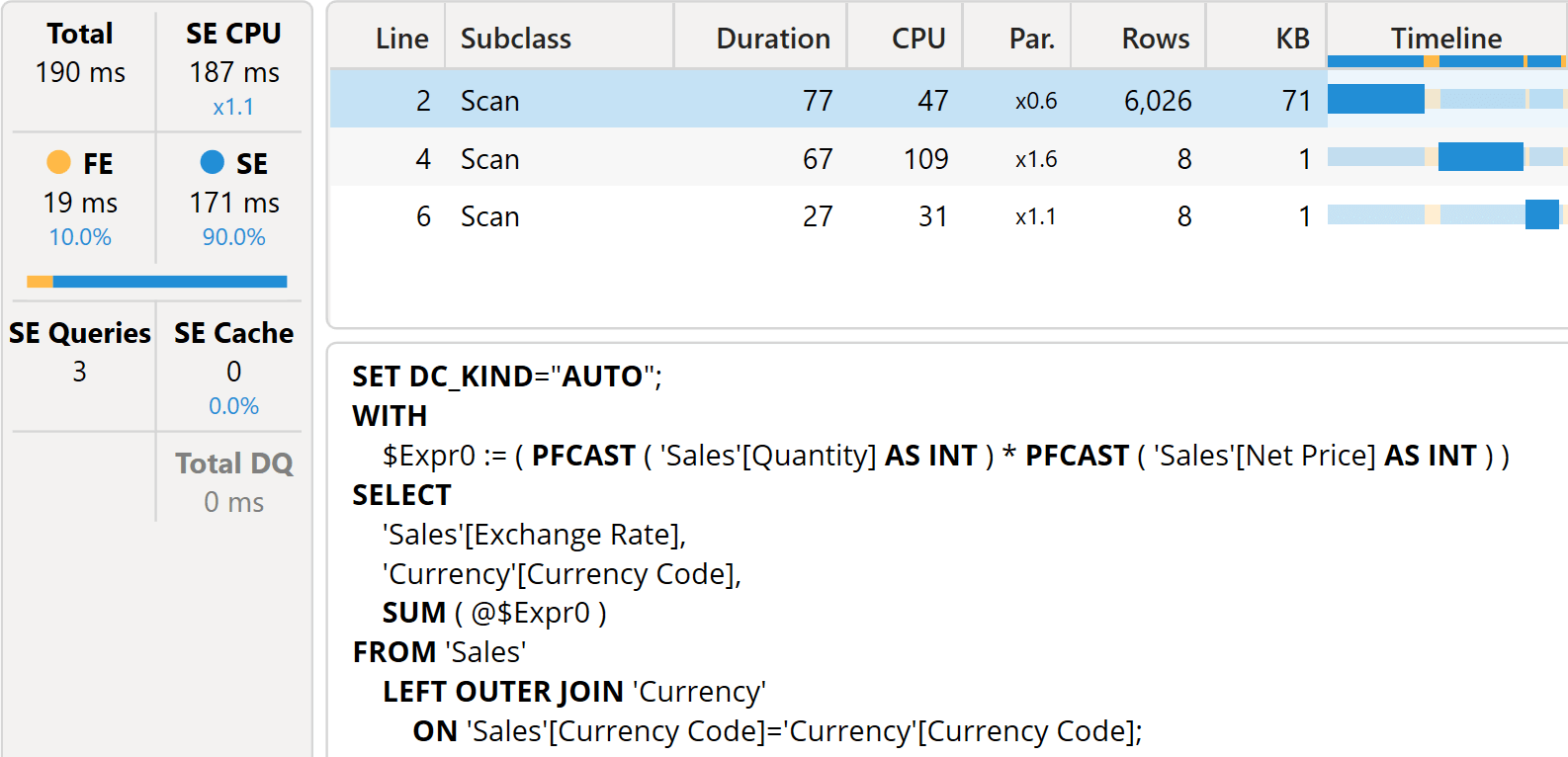
The storage engine CPU went from more than four seconds to one-fifth of a second. At the same time, the number of rows generated in the datacache is largely increased: from eight rows to more than six thousand. The reason is the additional grouping by Sales[Exchange Rate] required by the formula.
Hence, paying attention to these small details might make a significant difference when performing multiplications between decimal and fixed decimals.
Precision impact of data type conversion
From a performance point of view, there is nothing more to say. However, we want to conclude the article with a word of warning for the brave readers who have reached this point. If one wants to check whether the two formulas compute the same number, to be on the safe side, another nasty surprise is waiting for them. Despite being semantically identical, the two formulas show quite a significant difference. Indeed, executing the following query shows the issue:
DEFINE
MEASURE Sales[Original Amount 1] =
SUMX (
Sales,
Sales[Exchange Rate] * Sales[Quantity] * Sales[Net Price]
)
MEASURE Sales[Original Amount 2] =
SUMX (
VALUES ( Sales[Exchange Rate] ),
Sales[Exchange Rate] * [Sales Amount]
)
EVALUATE
ADDCOLUMNS (
SUMMARIZE (
Sales,
'Currency'[Currency Code]
),
"Original Amount 1", [Original Amount 1],
"Original Amount 2", [Original Amount 2]
)
The results for Original Amount 1 and Original Amount 2 are quite different. In this specific case, because it is fixed decimals we are dealing with, the error introduced would be the same as that present by performing the conversion at the transaction level. However, this is specific to our calculation. In general, the numbers may well be very different.
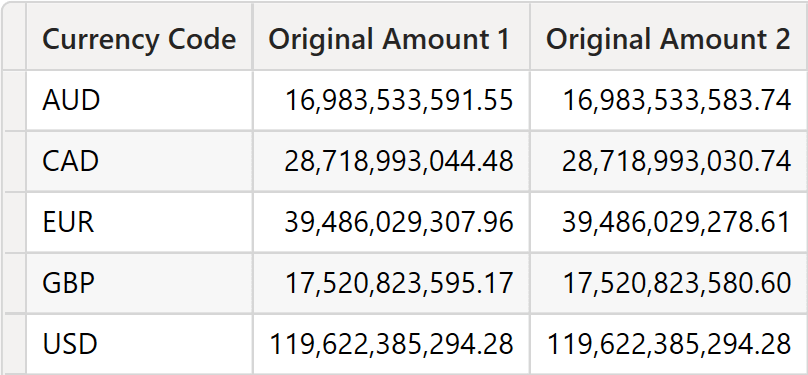
You might be surprised, outraged, maybe bewildered. However, this behavior is entirely expected. We somewhat take for granted that the value of Original Amount 1 is the correct one, but this is only because it is the first number we witnessed. Both values are correct, meaning that both include some rounding errors. Moreover, both values originated from values which, in turn, are rounded. When the conversion between the original currency was made in the database, there was already a rounding error. That error has been propagated. Then, each time we perform a multiplication, the error becomes larger. When we sum 225 million values, each of which contains a tiny error, the result simply cannot be correct. None of the numbers you have seen so far are correct. To be honest, there are no ways to obtain a perfect number because of the original rounding that happened at the database level.
Moreover, the latest formula reduces the number of multiplications to 6,000, compared to the 225 million of the first. Therefore, the value of the last formula is more correct (or less wrong?) than the original formula’s.
These issues happen all the time on a large model. Tiny errors introduced at some point in the process may result in larger errors in the end. This is to be expected, and a good BI professional needs to understand these issues well to explain the topic to the users.
If you are still surprised, look at the following query, showing two different versions of the same code where the only difference is the order of the multiplications:
DEFINE
MEASURE Sales[Original Amount 1] =
SUMX (
Sales,
Sales[Exchange Rate] * Sales[Quantity] * Sales[Net Price]
)
MEASURE Sales[Original Amount 2] =
SUMX (
Sales,
Sales[Exchange Rate] * Sales[Net Price] * Sales[Quantity]
)
EVALUATE
ADDCOLUMNS (
SUMMARIZE (
Sales,
'Currency'[Currency Code]
),
"Original Amount 1", [Original Amount 1],
"Original Amount 2", [Original Amount 2],
"USD Amount", [Sales Amount]
)
The following is the result.
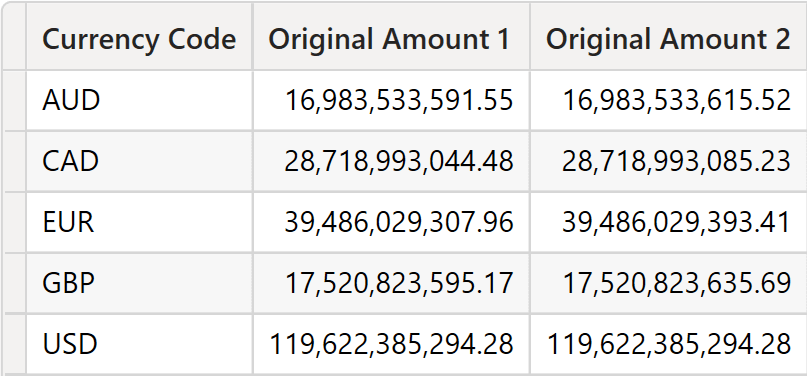
Again, the numbers are different, and they could be more accurate. There are many more examples of rounding issues that may surprise you; we show some of these in the Mastering Tabular Video Course.
However, be mindful that if those numbers are surprising… this means you have yet to learn how computers store numbers, how they perform math, and some of the many extremely hard challenges that engineers have to solve to perform even simple calculations. Once you master these concepts, these small errors are no longer surprising. Knowing the reality can only make you a better developer and empower you to avoid wasting time trying to fix a number that – simply – cannot be fixed.
 Marco Russo & Alberto Ferrari
Marco Russo & Alberto Ferrari