DAX offers the RANKX function to compute ranking over a table, based on measures or columns. One limitation of RANKX is that it is only capable of ranking using a single expression. Oftentimes it is necessary to use multiple columns to obtain a ranking, either because the business requirement dictates it, or because you want to rank ties with different criteria.
As a demonstration, we rank customers based on their purchase volume. To artificially introduce ties, we use the Rounded Sales measure, that rounds the sales amount to the nearest multiple of one thousand. Using Rounded Sales, several customers show the same amount of 6,000.00. Because they are ties, their ranking must now be defined by alphabetical order based on their names.
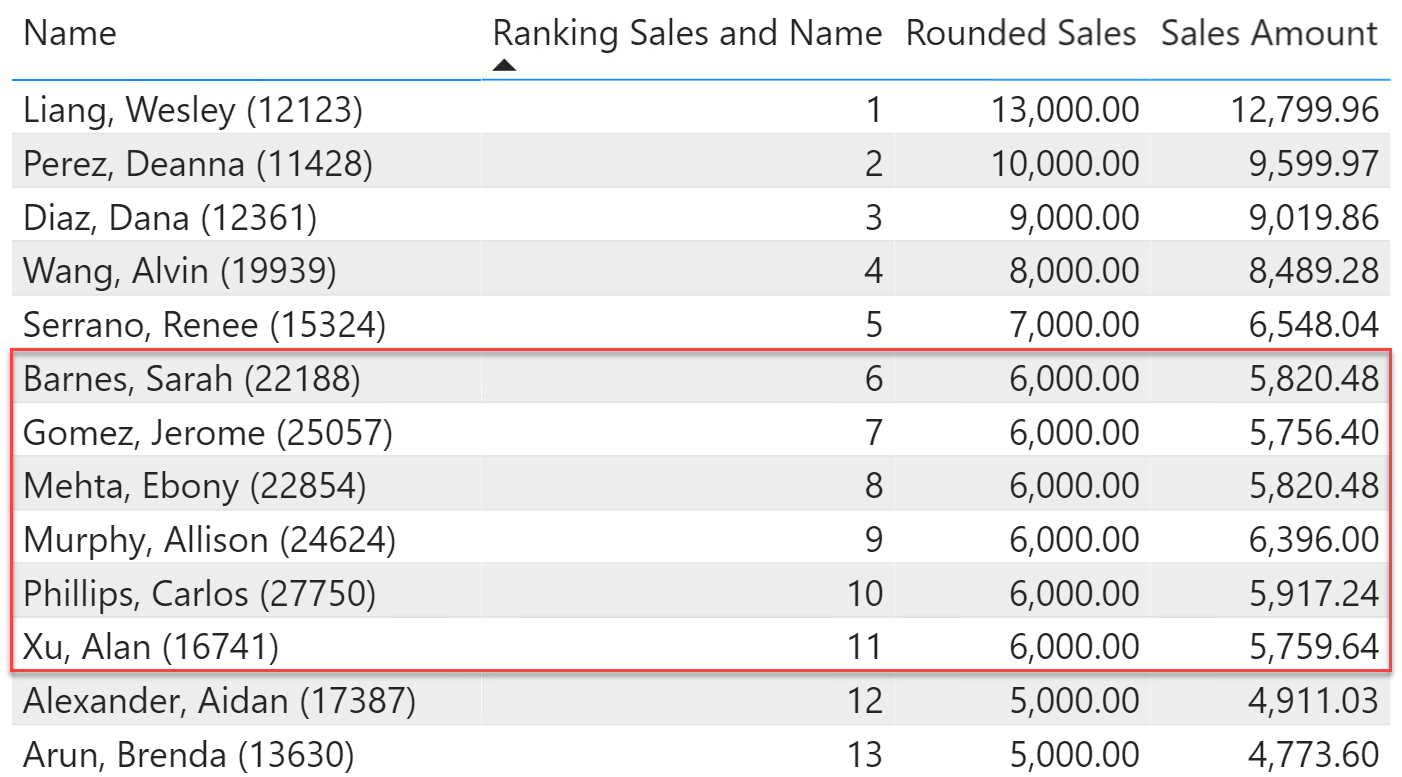
The code to author is different based on two details:
- Whether you want a static ranking (that is, a calculated column) or a dynamic ranking (driven by a measure). A column is simpler, a measure is harder.
- The data type of the column used for the ranking. In the previous figure we showed alphabetical sorting, which is why we used a string. If you use a number for the second ranking column, the code is much simpler.
Based on the previous assumptions, the article shows four different versions of the same calculation, presented in order of increasing complexity.
Let us start outlining the overall algorithm. We want to rank customers based on two values. We call the most relevant value HIGH (Rounded Sales, in our example) and the less relevant value LOW. HIGH is the same in all our examples, whereas LOW can be either the customer code or the customer name. The customer code is a meaningless number; its only advantage is the fact that it is an integer, therefore easier to handle. The customer name is much more useful, but it poses the added challenge that we need to transform it into an integer before using it in our formulas.
Because RANKX can rank based on a single expression, we use a combination of HIGH and LOW where HIGH is shifted so that the lowest HIGH is higher than the highest LOW. This can be accomplished by using HIGH * MAX ( LOW ) + LOW as the expression for the ranking. This way, a value of HIGH equal to 1 is still larger than the maximum LOW. With equal values for HIGH, the ranking is based on LOW.
Static ranking on Rounded Sales and customer code
If the ranking is static, we rely on calculated columns for the entire implementation. First, we create a calculated column to store the value of Rounded Sales for each customer:
Customer Sales = [Rounded Sales]
Then, another calculated column stores the ranking. The ranking is computed by first retrieving the maximum code (LOW) and then using this value as a multiplier for HIGH (Customer Sales):
Ranking Sales and Code =
VAR MaxCustomerCode = MAX ( Customer[Customer Code] )
VAR Result =
RANKX (
ALL ( Customer ),
Customer[Customer Sales] * MaxCustomerCode + Customer[Customer Code]
)
RETURN
Result
It is worth to note that ALL on Customer is not needed in a calculated column. Still, we prefer to use it to make it more evident that the ranking takes place on all the customers. The readability of the code is one of our top priorities.
The customer code is not visible to the user – it is used only to create unique rankings. Therefore, we do not worry about which customer comes first. This small detail will require additional work later, when we use the customer name – therefore we will want the customer with an earlier name to be ranked higher.
Static ranking on Rounded Sales and customer name
When the second ranking column is a string, like the customer name, a simple multiplication is no longer an option. You cannot multiply a number by a string. That said, we can convert the customer name into a number by using an additional calculated column that computes the ranking of the customer by name.
The solution uses the Customer Sales calculated column introduced earlier, and then it creates another calculated column we will call Name Ranked that computes the ranking of the customer by name:
Name Ranked = RANKX ( ALL ( Customer ), Customer[Name],, DESC, DENSE )
It is important to note that we explicitly used DESC for the ranking. The reason is that we want a customer with a name that comes first in alphabetical order to be ranked with a higher integer value. By using DESC, a customer named Marco is ranked better than a customer named Alberto. Being ranked better, Marco’s Name Ranked is lower than Alberto’s. The Name Ranked value is used later, in the next (and final) ranking operation. Marco’s value being lower, it will be ranked lower than Alberto in the final result. Therefore, in the end Alberto comes before Marco, following the natural alphabetical order:
Ranking Sales and Name =
VAR MaxCustomerName = MAX ( Customer[Name Ranked] )
VAR Result =
RANKX (
ALL ( Customer ),
Customer[Customer Sales] * MaxCustomerName + Customer[Name Ranked]
)
RETURN
Result
This latter calculated column is identical – in structure – to the ranking in the previous example. Because it uses the Name Ranked column, the algorithm is the same: it is ranking two numbers.
Dynamic ranking on Rounded Sales and customer code
If you need a dynamic ranking, then you need to author the code in a measure. A measure cannot rely on calculated columns for a dynamic calculation. Therefore, using the Customer Sales calculated column is no longer an option.
Ranking in a measure is a dangerous operation: if you do not pay attention to small details while writing the code, it can easily turn into a tremendously slow calculation. The key is to perform most of the calculations with variables that are independent from the individual cell being computed. Those variables are evaluated only once by the optimizer and then used in the evaluation of all the individual cells:
Ranking Code Measure :=
VAR RoundedSales = [Rounded Sales]
RETURN IF (
HASONEVALUE ( Customer[Name] ) && ( RoundedSales > 0 ),
VAR MaxCustomerCode =
CALCULATE ( MAX ( Customer[Customer Code] ), REMOVEFILTERS () )
VAR LookupTable =
ADDCOLUMNS (
ALLSELECTED ( Customer ),
"@CustomerSales",
[Rounded Sales] * MaxCustomerCode + Customer[Customer Code]
)
VAR CurrentValue =
RoundedSales * MaxCustomerCode + SELECTEDVALUE ( Customer[Customer Code] )
VAR Ranking =
RANKX ( LookupTable, [@CustomerSales], CurrentValue,, DENSE )
RETURN
Ranking
)
The measure looks complex, but it is rather simple in its structure.
First, it computes MaxCustomerCode using REMOVEFILTERS to retrieve the maximum over the entire model. By using REMOVEFILTERS, the result is a constant value that does not even require a query to be computed.
Second, the code creates the LookupTable variable. LookupTable creates a temporary copy of the Customer Sales calculated column we used in the static ranking examples. This temporary table is later used in RANKX, to rank the value of HIGH and LOW for the current customer against the same expression computed over the lookup table.
Dynamic ranking on Rounded Sales and customer name
The last and more complex example is the ranking by name in a measure. In this last scenario we need not only to compute a temporary column for the customer sales; we also must compute another temporary column for the Name Ranked column, needed to transform the name into a number:
Ranking Name Measure :=
VAR RoundedSales = [Rounded Sales]
RETURN IF (
HASONEVALUE ( Customer[Name] ) && ( RoundedSales > 0 ),
VAR CustomersWithRankedName =
ADDCOLUMNS (
ALLSELECTED ( Customer ),
"@NameRanked", RANKX ( ALLSELECTED ( Customer ), Customer[Name],, DESC, DENSE )
)
VAR MaxCustomerNameRanked =
MAXX ( CustomersWithRankedName, [@NameRanked] )
VAR LookupTable =
ADDCOLUMNS (
CustomersWithRankedName,
"@CustomerSales",
[Rounded Sales] * MaxCustomerNameRanked + [@NameRanked]
)
VAR CurrentName =
SELECTEDVALUE ( Customer[Name] )
VAR CurrentNameRanked =
RANKX ( ALLSELECTED ( Customer ), Customer[Name], CurrentName, DESC, DENSE )
VAR CurrentValue = RoundedSales * MaxCustomerNameRanked + CurrentNameRanked
VAR Ranking =
RANKX ( LookupTable, [@CustomerSales], CurrentValue,, DENSE )
RETURN
Ranking
)
As you see, despite being long this measure is nothing but a combination of the techniques outlined earlier in this article.
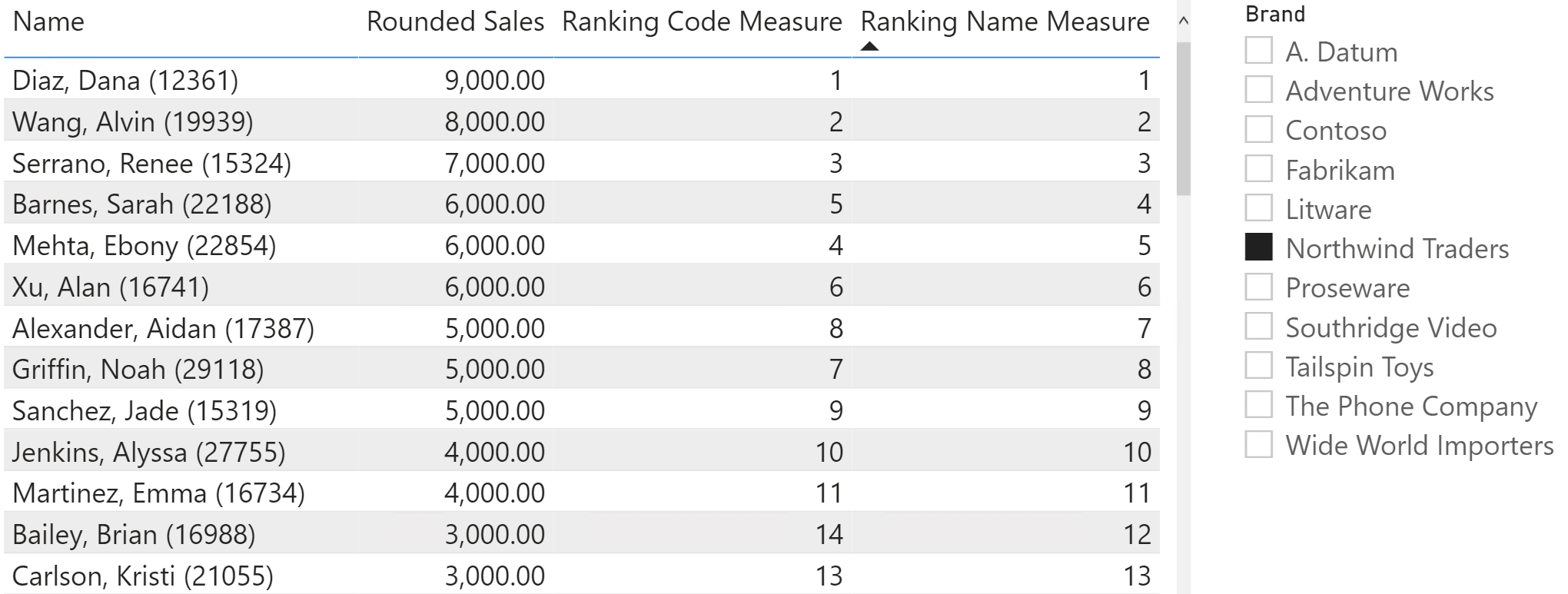
In the last figure you can appreciate that the ranking by code provides unique values, but the sort order is not relevant to the user. On the other hand, the Ranking Name Measure combines a sorting by both Rounded Sales and Name at the same time.
Conclusions
Although RANKX does not provide a built-in functionality to rank by different columns, you can obtain the desired behavior by mixing DAX with some creativity and a little math.
Returns the rank of an expression evaluated in the current context in the list of values for the expression evaluated for each row in the specified table.
RANKX ( <Table>, <Expression> [, <Value>] [, <Order>] [, <Ties>] )
Returns the largest value in a column, or the larger value between two scalar expressions. Ignores logical values. Strings are compared according to alphabetical order.
MAX ( <ColumnNameOrScalar1> [, <Scalar2>] )
Returns all the rows in a table, or all the values in a column, ignoring any filters that might have been applied.
ALL ( [<TableNameOrColumnName>] [, <ColumnName> [, <ColumnName> [, … ] ] ] )
Clear filters from the specified tables or columns.
REMOVEFILTERS ( [<TableNameOrColumnName>] [, <ColumnName> [, <ColumnName> [, … ] ] ] )
 Alberto Ferrari
Alberto Ferrari