Introducing RANKX in DAX

Ranking is one of the most frequent calculations in Power BI reports. Needing to determine the top products, countries, customers and such is extremely common. RANKX offers a powerful and very fast way to produce ranking. Nonetheless, its use takes some understanding.

In this article we introduce the RANKX function and provide a few interesting examples of how it can be used. RANKX is not a complex function to learn. Nonetheless, most newbies find it intimidating because they do not fully grasp its internals. Once they learn exactly how RANKX works, its use becomes really simple.

For educational purposes, we follow an unusual approach in showing the use of RANKX: first an example with the most commonly-used pattern. Then based on that pattern, we explain the reasons behind the choice of functions used. Finally, we expand on your new knowledge with further considerations.

We want to create the Ranking on Brand measure depicted in the figure below, which computes the ranking of different brands based on their sales amount.

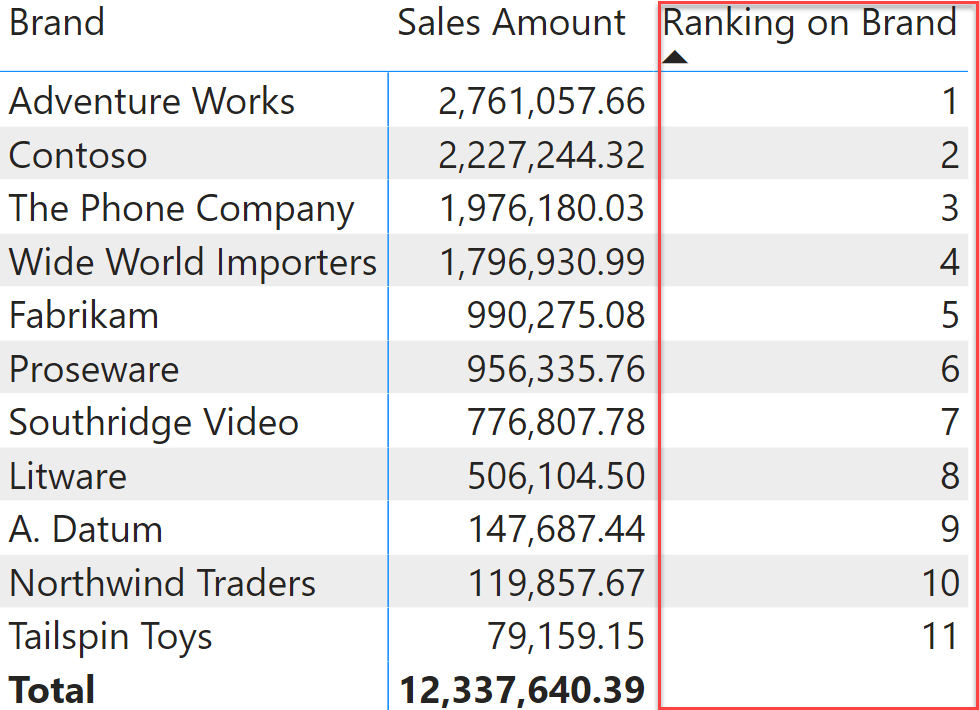
The pattern to use is the following:

Measure in Sales table

Ranking on Brand :=
IF (
    ISINSCOPE ( 'Product'[Brand] ),
    RANKX (
        ALLSELECTED ( 'Product'[Brand] ),
        [Sales Amount]
    )
)

There are three important details in this formula:

The use of ISINSCOPE to avoid showing a value at the grand total level, and to ensure the ranking is computed accurately;
The presence of ALLSELECTED as the first argument of RANKX, to retrieve the list of brands visible in the matrix;
The RANKX function, used to compute the ranking.

It is important to understand the reason for each of these details. We start by describing what RANKX does, and then we explain why ISINSCOPE and ALLSELECTED are relevant.

RANKX works by following three steps:

It creates the lookup table by iterating over its first argument and evaluating the second argument in the row context generated by the iteration. The lookup table is then sorted in descending order (by default, this can be changed).
It computes the second argument outside of the iteration, in the filter context where the formula is being computed.
It searches for the place where to put the result of (2) in the lookup table computed during (1), following the sort order chosen during (1).

It might be surprising for the reader to read such an intricate algorithm, to describe the process of ranking. It is important to understand the algorithm well if we want to obtain the best out of RANKX. Let us follow the algorithm on the matrix depicted earlier, focusing on the value for Contoso which sits at rank 2.

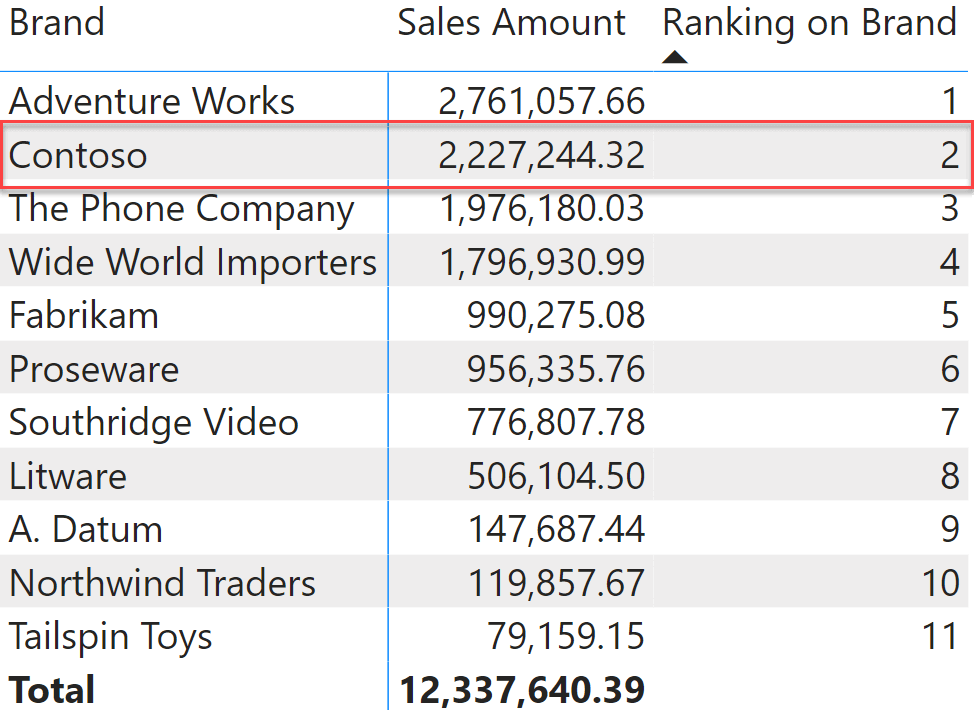
The code executed is the following snippet, focused only on RANKX:

RANKX (
    ALLSELECTED ( 'Product'[Brand] ),
    [Sales Amount]
)

The first argument of RANKX is ALLSELECTED ( Product[Brand] ). ALLSELECTED returns a table containing the values of the Brand column visible in the matrix, therefore it produces a table with all the possible brands, which is returned to RANKX.

RANKX starts iterating the table with all the brands, and for each row it computes the Sales Amount measure. During the iteration there is a row context active, and because Sales Amount is a measure, it is automatically surrounded by CALCULATE. CALCULATE performs the context transition, thus transforming the row context into a filter context. Therefore, during the iteration, RANKX computes Sales Amount for each brand. The resulting table looks like this:

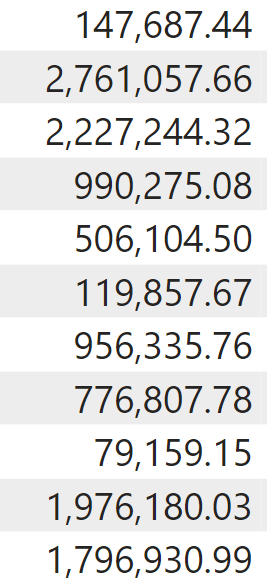
There are a couple of interesting details in the table we obtained. First, the table has no header. It contains a column with no name. In other words, it is just a list of values. Second, the table is not sorted. So far, the sort order has not been defined. RANKX performs the sorting of the table as the last part of its first step. One of the arguments of RANKX defines whether the sorting is ascending or descending, and as we will see later it changes the result of RANKX. We use the default descending order for now.

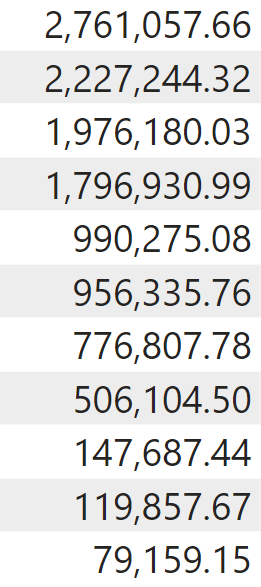
The first step of RANKX is completed, the lookup table is ready. Time to execute the second step. RANKX computes the second argument (Sales Amount) outside of the iteration. Therefore, it executes Sales Amount in the filter context of the current cell, which is filtering Contoso. Therefore, it computes the value of Sales Amount for Contoso: 2,227,244.32.

The third step is to search for the position of 2,227,244.32 in the lookup table already sorted. It turns out that it fits perfectly in second place. Hence, the result of 2.

As promised earlier, let us now discover why the two other ingredients are important. First, ALLSELECTED. The first argument of RANKX needs to produce a table that contains all the values we want to rank. If you forget to ignore the filter context and use VALUES instead of ALLSELECTED, then you end up authoring the Ranking Wrong (1) measure:

Measure in Sales table

Ranking Wrong (1) := 
IF (
    ISINSCOPE ( 'Product'[Brand] ),
    RANKX (
        VALUES ( 'Product'[Brand] ),
        [Sales Amount]
    )
)

The result is an unfortunate, constant value of 1.

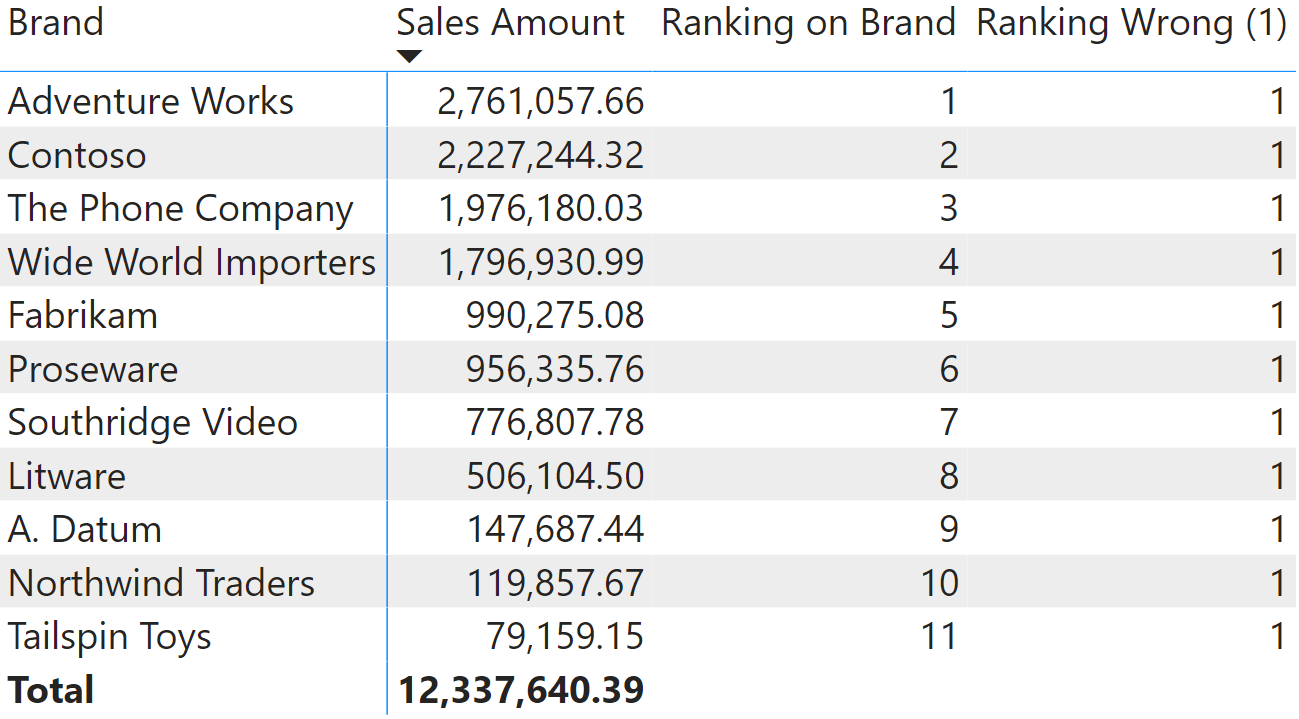
The reason behind the constant value of 1 is that VALUES, for each cell, returns a table with a single row only. Therefore, the lookup table contains only one row with the sales amount of the brand visible currently. Hence, the result is always 1.

We could have used ALL instead of ALLSELECTED. ALLSELECTED guarantees a better behavior in the presence of slicers that reduce the number of brands visible to the matrix.

The other important aspect is to protect the code with ISINSCOPE. If we had not protected the code with ISINSCOPE, then we would have computed the value for the grand total too. At the grand total, the lookup table is still computed correctly, because of the context transition. However the value in step (2) would be the grand total of Sales Amount, which is 12,337,640.39. A number that seems outrageously large in comparison to the other values you are working with, will always rank first, because it is for sure larger than any value in the lookup table. Here is what the matrix would look like if the code were not protected with ISINSCOPE.

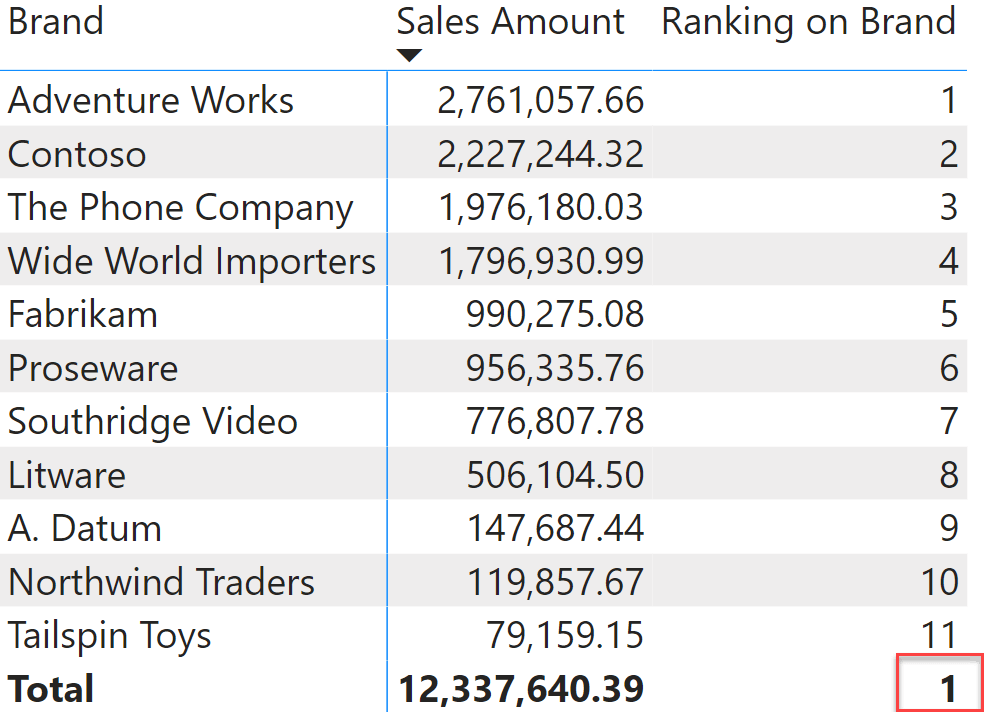
Besides, in this example we used ISINSCOPE because the RANKX function was expected to be used brand by brand. You always need to protect RANKX with at least HASONEVALUE, to make sure that the value computed in (2) actually has the same granularity as the values computed during step (1). If it so happens that the value computed in (2) includes multiple brands, then the ranking will be wrong. Protecting your code so that your measures never compute an inaccurate number is an important part of your DAX skills.

We have shown RANKX with two arguments, which is the most frequently-used pattern. RANKX accepts three more arguments:

The third argument is an optional expression that is used during step (2). By default, RANKX uses the same expression to build the lookup table and the value to search for. In some advanced scenarios, the two expressions might be different – for example when ranking the sales amount against a given configuration table.
The fourth argument is the order to be used at the end of step (1): it can be ascending or descending. By default, the order is descending.
The fifth argument can be SKIP (by default) or DENSE. When it is SKIP, the lookup table is computed and used as is. When DENSE is specified, at the end of step (1) DAX removes duplicates from the lookup table. The net effect is that when the lookup table contains duplicates, these are counted as only one value.

Let us see an example where the third argument can be useful. Imagine we want to find the segment which the sales amount of a brand belongs to, using a segmentation table like the one depicted here named Sales Segments.

If we want to use this table as the lookup table, we need to use ‘Sales Segments'[Sales] as the second argument (used during the building of the lookup table) and Sales Amount to compute the value to search for:

Measure in Sales table

Segment :=
IF (
    ISINSCOPE ( 'Product'[Brand] ),
    RANKX (
        'Sales Segments',
        'Sales Segments'[Sales],
        [Sales Amount]
    )
)

Here is the result of the Segment measure, along with the Sales Segment table sorted descending to make it easier to picture the lookup table.

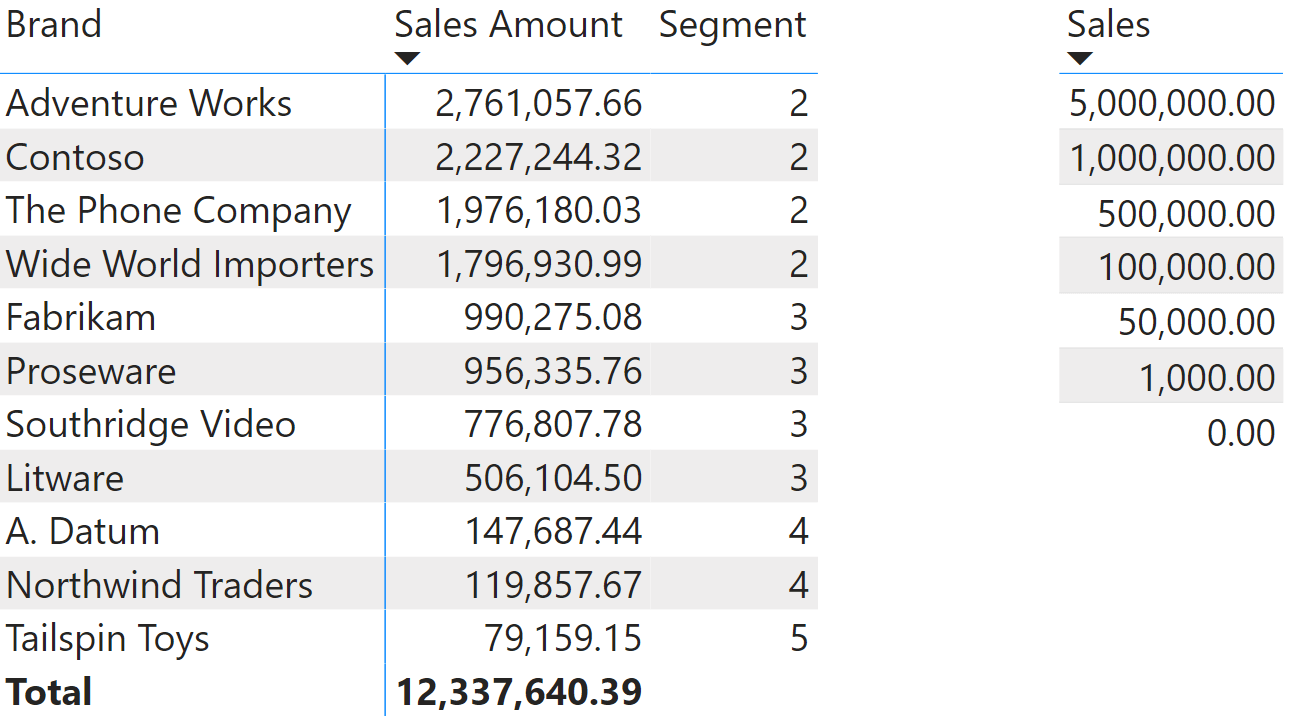
To appreciate the use of the last argument of RANKX (DENSE or SKIP) we need to introduce ties in the ranking, in order to obtain duplicates in the lookup table. We can use a new measure, Rounded Sales, that rounds the value of Sales Amount to a multiple of 500,000 using MROUND:

Measure in Sales table

Rounded Sales := MROUND ( [Sales Amount], 500000 )

Because of the rounding, the lookup table now contains several duplicates and you can control whether to keep them in the lookup table (SKIP) or to remove them at the end of step 1 (DENSE). Here are the two measures used to test the behavior:

Measure in Sales table

Ranking DENSE :=
IF (
    ISINSCOPE ( 'Product'[Brand] ),
    RANKX (
        ALLSELECTED ( 'Product'[Brand] ),
        [Rounded Sales],
        ,
        ,
        DENSE
    )
)

Measure in Sales table

Ranking SKIP :=
IF (
    ISINSCOPE ( 'Product'[Brand] ),
    RANKX (
        ALLSELECTED ( 'Product'[Brand] ),
        [Rounded Sales],
        ,
        ,
        SKIP
    )
)

As you see, the results vary in the way values of Fabrikam and below are computed, due to duplicates in the lookup table.

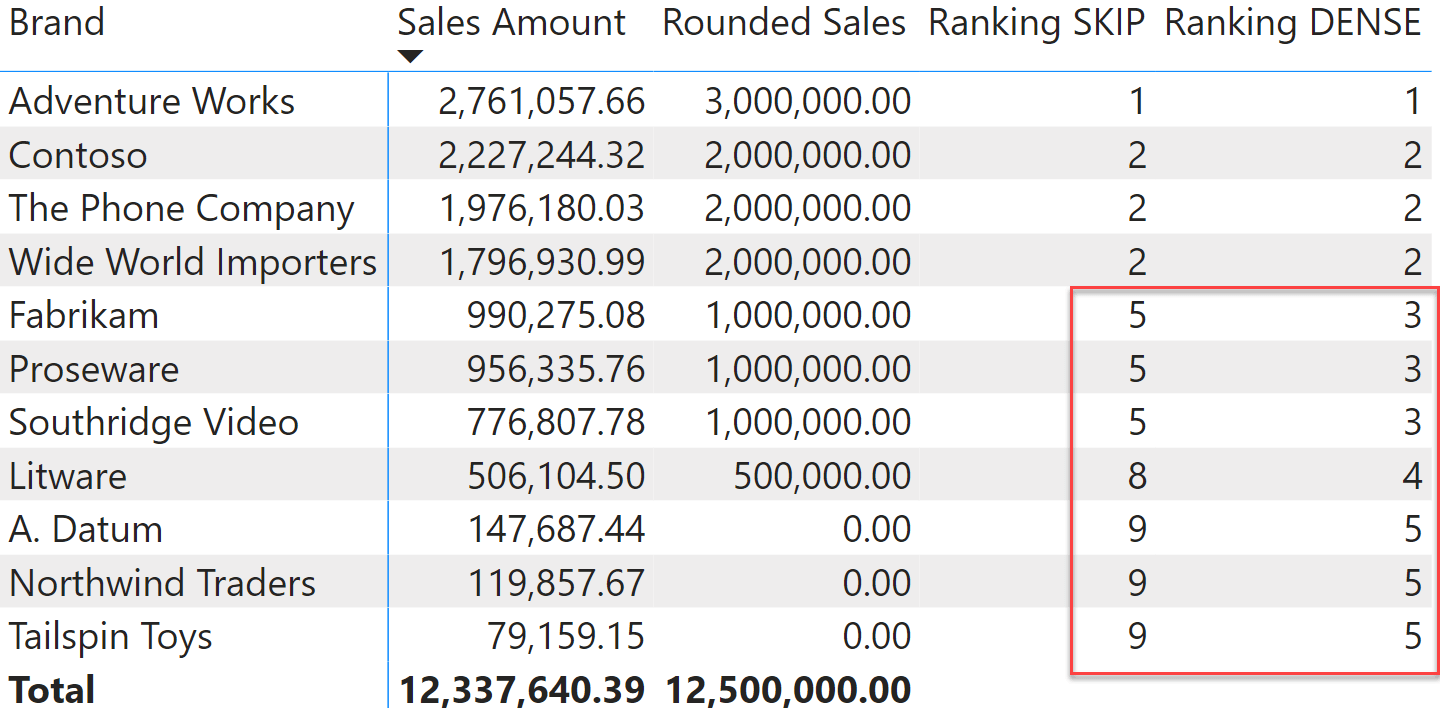
RANKX is a very powerful and fast function in DAX. Learning how it works internally provides you with the mastery required to write DAX with all confidence that the values computed are correct. This is true not only for RANKX. Indeed, RANKX relies on the concepts of context transition, iterations, row context, and filter context. These are foundational topics of DAX that you will find everywhere, and thus that you need to learn and master to become a proficient DAX developer.

If you are not familiar with these concepts yet, you can start by reading our DAX 101 series of articles and videos, or go straight to the more comprehensive trainings we offer at SQLBI to start joining the family of DAX experts.