Understanding ALLSELECTED

**********************
**********************
UPDATE 2018-02-05 : this article is outdated. Please read The Definitive Guide to ALLSELECTED instead, which contains updated information about ALLSELECTED.
**********************
**********************

Let us state this simple fact from the beginning: ALLSELECTED has no clues of what the user selected in the pivot table. ALLSELECTED does not even know that a pivot table exists. Therefore, how does it work?

ALLSELECTED removes the last filter generated from context transition.

The side effect of this operation is that—in most cases—it retrieves the original filter context. Unfortunately, this does not always happen and you might write formulas where you expect ALLSELECTED to compute a value (based on the naïve definition of ALLSELECTED) and you end up with an unexpected result.

In order to understand the behavior of ALLSELECTED, you have to refine a bit the knowledge about context transition. You probably know that context transition transforms all existing row contexts into equivalent filter contexts. Thus, you know that, after context transition, all row contexts are replaced with a single filter context containing all the equivalent filters. This is not completely correct. In reality, context transition generates two new filter contexts: one containing the iterated table, one containing the current row of the same table. Let us elaborate on this analyzing the following, simple measure:

AverageSales :=
AVERAGEX ( 
    Customer,
    CALCULATE ( SUM ( Sales[Quantity] ) )
)

During iteration the measure invokes CALCULATE, thus context transition happens. The engine transforms the current row on Customer into two filter contexts, that are applied one after the other:

The first one contains Customer
The second one contains the currently iterated row on Customer

This behavior is transparent to your code in most cases. The reason is that the two filters are placed one after the other in the stack of filter contexts. Thus, the last one (containing a single customer) is always more restrictive than the previous one, effectively hiding it. We refer to the first filter as the outer filter, while the second one is the inner filter. When CALCULATE ends, both filters are removed from the stack. Thus, your code typically ignores the existence of the outer filter, because it has no effect during CALCULATE and no effect after CALCULATE ends.

Keep in mind that this behavior always happens, even if you do not notice it. Look at the following example:

AverageSalesInEurope :=
AVERAGEX ( 
    FILTER ( Customer, Customer[Contintent] = "Europe" ),
    CALCULATE ( SUM ( Sales[Quantity] ) )
)

In this case, iteration happens for only the customers in Europe. Thus the two filters are:

Outer: customers in Europe
Inner: currently iterated customer from the ones in Europe

Again, the currently iterated one is more restrictive than the list of all customers in Europe, thus you normally ignore the existence of the outer filter. You can safely ignore it, until you start using ALLSELECTED. In fact, ALLSELECTED will remove the more restrictive filter (inner), leaving the outer one working. This behavior is somewhat complex to follow, until you get used to it, so some examples might help in learning it better.

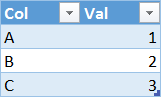
In order to understand the behavior of ALLSELECTED, we use a very simple data model, containing a single table (called T) with only three rows and two columns (Col and Val):

Based on this table, you can easily create a pivot table with a slicer that selects only two rows and the Sum of Val in the value area:

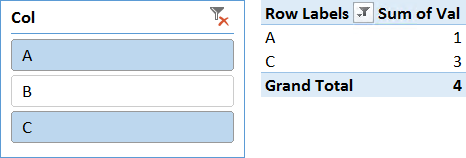
There is nothing special here. We filter two values, and all the numbers are correct. Now you can define a new measure, using this code:

SumAllSelected :=
CALCULATE (
    SUM ( Table[Val] ), 
    ALLSELECTED ( ) 
)

Intuitively, you expect this measure to compute the value of 4 for all the rows. This is because you use ALLSELECTED without parameters, which means you want to retrieve the original filter context. In fact, the result is correct:

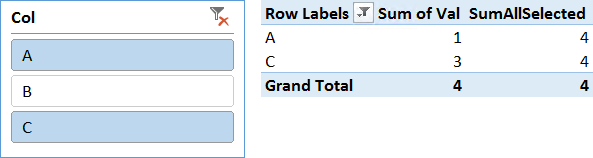
Before moving on, we need to be a bit more accurate about how DAX computed the formula in the cells. There are two different steps in evaluating the full PivotTable:

One step computes the values for the individual rows
One step computes the values for the grand total

The reason for this is that the individual rows contain a filter on T[Col] that filters a single value (either A or C), whereas at the grand total the filter context contains both A and C. Both steps run under a filter created by the slicer.

In reality, the code that is executed is MDX, not DAX. Nevertheless, for the sake of this example, we use DAX to make it easier to follow the flow of execution. What you see here is a very good approximation of what happens under the cover.

The code for the individual rows is similar to this:

EVALUATE
CALCULATETABLE (
    ADDCOLUMNS (
        VALUES ( T[Col] ),
        "Sum of Val", [Sum of Val],
        "SumAllSelected", [SumAllSelected]
    ),
    OR ( T[Col] = "A", T[Col] = "C" )
)

On the other hand, the code for the grand total looks like this:

EVALUATE
CALCULATETABLE (
    ROW (
        "Grand Total Sum of Val", [Sum of Val],
        "Grand Total SumAllSelected", [SumAllSelected]
    ),
    OR ( T[Col] = "A", T[Col] = "C" )
)

As you can see, even if your original code in the measures does not contain any iteration, there is a hidden iteration introduced by ADDCOLUMNS during the evaluation of the rows. Moreover, note that this iteration is not present during the evaluation of the grand total rows. At all effect, they are two different steps of execution with different semantics.

Now, let us focus on what happens during the evaluation of SumAllSelected for the individual rows. The outer CALCULATETABLE sets the original filter context to A or C. Then ADDCOLUMNS starts to iterate over the VALUES of T[Col], which contains A and C. When it is on A, it performs context transition, because it is calling a measure (SumAllSelected). This context transition creates two filters:

The outer one, containing the currently iterated table, i.e. (A, C)
The inner one, containing the currently iterated row, i.e. (A)

At this point, DAX evaluates SumAllSelected which executes again CALCULATE, this time invoking it with ALLSELECTED. ALLSELECTED removes the last filter context generated from context transition, that is the inner one, making the outer one visible. Because the outer filter context contains (A, C), it computes the sum of A and C together, generating the visual total, as expected.
On the grand total, on the other hand, there is no filter context generated by context transition. Thus, ALLSELECTED has nothing to do, and it is ignored. Because the outer CALCULATETABLE is still in effect, the filter context still contains (A, C), generating, again, the visual total.

You are already familiar with most of these evaluation steps. Probably the only new information you are gathering at this point is the presence of the hidden row context generated during the iteration over the fields you put on rows and columns of the pivot table. You do not really need to care about that row context in most scenarios, because the engine generates it and quickly transforms it into a filter context. Thus, from inside your code, you cannot access it. ALLSELECTED is the only function that interacts with it and this is the reason we are speaking in so much detail about the evaluation process of a pivot table here.

What is important to learn and to understand is that ALLSELECTED shows the visual totals because of the specific format of the query executed by the engine when it resolves a query coming from a pivot table. However, ALLSELECTED by itself has nothing to do with visual totals.

So far, it seems as if we are providing a complex explanation to a very simple behavior. To some extent this is true because you will probably use ALLSELECTED for a long time without ever having to recall this theory. Nevertheless, look what happens if you write a measure that contains an iteration and another context transition, as in the following measure:

SumxAllSelected := SUMX ( T, [SumAllSelected] )

It is worth remembering the code of SumAllSelected:

SumAllSelected :=
CALCULATE (
    SUM ( T[Val] ), 
    ALLSELECTED( ) 
)

At this point, the scenario is much more complex. We have the hidden iteration created by the pivot table, and inside it, another iteration created by SUMX that performs an additional context transition. The result is surprising:

You probably would expect SumxAllSelected to return 4 in each inner row of the pivot table and 8 at the grand total, because it iterates over T (which shows one row in the inner cells and two rows at the grand total) and sums a measure of which we already know the result: it should be 4. Surprisingly, the value at the grand total makes sense, whereas the values in the inner cells seem completely wrong. Let’s examine what happened by expanding the code. Since we are interested in only the last measure (SumxAllSelected), we are using a somewhat simplified version of the code, which ignores other measures:

EVALUATE
CALCULATETABLE (
    ADDCOLUMNS (
        VALUES ( T[Col] ),
        "SumxAllSelected", [SumxAllSelected]
    ),
    OR ( T[Col] = "A", T[Col] = "C" )
)

EVALUATE
CALCULATETABLE (
    ROW (
        "Grand Total SumxAllSelected", [SumxAllSelected]
    ),
    OR ( T[Col] = "A", T[Col] = "C" )
)

In order to understand it even better, let us fully expand the code of SumxAllSelected to its definition, focusing on the portion that computes the individual rows:

EVALUATE
CALCULATETABLE (
    ADDCOLUMNS (
        VALUES ( T[Col] ),
        "SumxAllSelected", 
        CALCULATE (
            SUMX (
                T,
                CALCULATE ( SUM ( T[Val] ), ALLSELECTED () )
            )
        )
    ),
    OR ( T[Col] = "A", T[Col] = "C" )
)

With the fully expanded code, it is now more evident that the innermost CALCULATE is executed when there are two nested row contexts: the first one generated by the outer ADDCOLUMNS and the inner one generated by SUMX. In reality, the outer one has already been converted into a filter context by CALCULATE when the inner row context starts.
In the next table you can see the set of filter contexts generated by the various calls right before the innermost CALCULATE is executed:

Function Call	Filter Context	Notes
CALCULATETABLE	(A, C)
CALCULATE when iterating ADDCOLUMNS	(A, C)	Table
	(A)	Row
CALCULATE when iterating SUMX	(A)	Table
	(A)	Row

In this scenario, the innermost CALCULATE invokes ALLSELECTED, that removes the last filter context generated by context transition. As you can easily check, this time ALLSELECTED does not restore the original filter context. Instead, it restores a context containing only A. This is the reason why the pivot table shows the value for A or B in the value rows. Moreover, it is worth to note that the filter restored is not the original one, because the iteration started in the measure hid the row context generated by the pivot table.

At the grand total level, things are different. In fact, the fully expanded code of the grand total looks like the following:

EVALUATE
CALCULATETABLE (
    ROW (
        "Grand Total SumxAllSelected", 
        CALCULATE (
            SUMX (
                T,
                CALCULATE ( SUM ( T[Val] ), ALLSELECTED () )
            )
        )
    ),
    OR ( T[Col] = "A", T[Col] = "C" )
)

In this case, the only iteration is the one introduced by SUMX. The innermost CALCULATE performs context transition, removing the row (either A or C) and restoring the table over which SUMX is iterating, namely a table containing both A and C. In fact, at the grand total, you see a value of 8, which is two times four.

As you see, until you understand exactly how ALLSELECTED works, it is nearly impossible to understand exactly how DAX computes its values. ALLSELECTED works in an intuitive way only when it is used as a filter in CALCULATE for a measure that is used directly inside a pivot table. However, as soon as you start mixing iteration, context transition and you generate deeper context transitions, ALLSELECTED starts to be very complex to follow and understand, up to a point where numbers seem to make no sense at all.

This article is a small example of the complete DAX description that you can read in our new book, The Definitive Guide to DAX.