The measure we want to compute is Rolling Avg 12M, which computes the rolling average of the Sales Amount measure over the last 12 months. When you project the rolling average on a chart, the resulting line is much smoother; it removes the spikes and drops that would make it difficult to recognize a trend in sales.
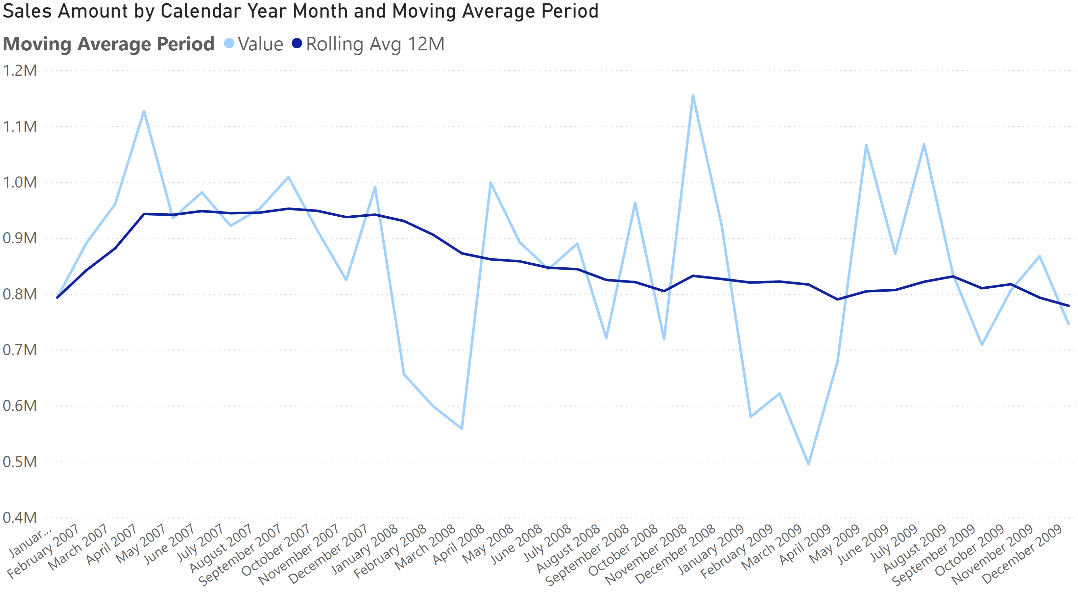
To compute the rolling average, we must compute Sales Amount over the last 12 months instead of the single month selected in the filter context. We use CALCULATE to extend the filter context to include the desired time period. The first part of the article shows the solution implemented in a regular measure. In the second part, we show how to implement a calculation group that can apply a rolling average to any existing measure.
Implementing a rolling average as a DAX measure
DATESINPERIOD is a DAX function designed for this goal. DATESINPERIOD returns a table with dates, starting from a given date and going down or up the desired period. There are three arguments of DATESINPERIOD:
- The Date column reference, to determine which column to return in the result;
- The reference date value, which is the starting point to determine the period;
- The period definition: it can be days, quarters, months, or years. The period definition requires two arguments to express for example “12 days” or “1 year”: a number and a unit of measure.
In the chart, each point represents a month. The selected month is included in the calculation. Therefore, if we’re going back one year for example the period starts from the end of the selected month and contains the previous 12 months, including the selected month. By using DATESINPERIOD, we first compute the requested period. This is accomplished by the following portion of the complete formula:
VAR NumOfMonths = 12
VAR LastCurrentDate =
MAX ( 'Date'[Date] )
VAR Period =
DATESINPERIOD ( 'Date'[Date], LastCurrentDate, - NumOfMonths, MONTH )
Once the time period is computed, we only need to extend the current filter context with the period and to compute the monthly average of sales:
Sales R12M =
VAR NumOfMonths = 12
VAR LastCurrentDate =
MAX ( 'Date'[Date] )
VAR Period =
DATESINPERIOD ( 'Date'[Date], LastCurrentDate, - NumOfMonths, MONTH )
VAR Result =
CALCULATE (
AVERAGEX (
VALUES ( 'Date'[Calendar Year Month] ),
[Sales Amount]
),
Period
)
VAR FirstDateInPeriod = MINX ( Period, 'Date'[Date] )
VAR LastDateWithSales = MAX ( Sales[Order Date] )
RETURN
IF ( FirstDateInPeriod <= LastDateWithSales, Result )
The filter obtained by DATESINPERIOD works at the day level, even though the rolling average calculation is defined at the month level. The DATESINPERIOD function allows you to create calculations at different granularities by just changing the first argument of AVERAGEX. For example, you can obtain the moving daily average thus working at the day granularity by using Date[Date] instead of Date[Calendar Year Month]:
VAR Result =
CALCULATE (
AVERAGEX (
VALUES ( 'Date'[Date] ),
[Sales Amount]
),
Period
)
Because the daily average produces a result that cannot be compared to the monthly amount we displayed on the initial chart, we do not provide a comparison of the numbers. We just wanted to bring to your attention different approaches that are possible. For example, if you want to optimize the performance while working at the month level, you can use a more efficient technique described for the moving average in Month-related calculations on the DAX Patterns website.
Implementing a rolling average as a DAX calculation group
We wrote the code of the measure in such a way that it is easy to transform it into a calculation item. Indeed, it is enough to replace Sales Amount with SELECTEDMEASURE to create a calculation item that transforms any measure into a rolling average.
In the example, we created a calculation group named Moving Average that contains different moving averages. Here is the code for the 3-months average:
CALCULATIONITEM 'PriceToUse'[Moving Average]."Rolling Avg 3M" =
VAR NumOfMonths = 3
VAR LastCurrentDate =
MAX ( 'Date'[Date] )
VAR Period =
DATESINPERIOD ( 'Date'[Date], LastCurrentDate, - NumOfMonths, MONTH )
VAR Result =
CALCULATE (
AVERAGEX (
VALUES ( 'Date'[Calendar Year Month] ),
SELECTEDMEASURE ()
),
Period
)
VAR FirstDateInPeriod = MINX ( Period, 'Date'[Date] )
VAR LastDateWithSales = MAX ( Sales[Order Date] )
RETURN
IF ( FirstDateInPeriod <= LastDateWithSales, Result )
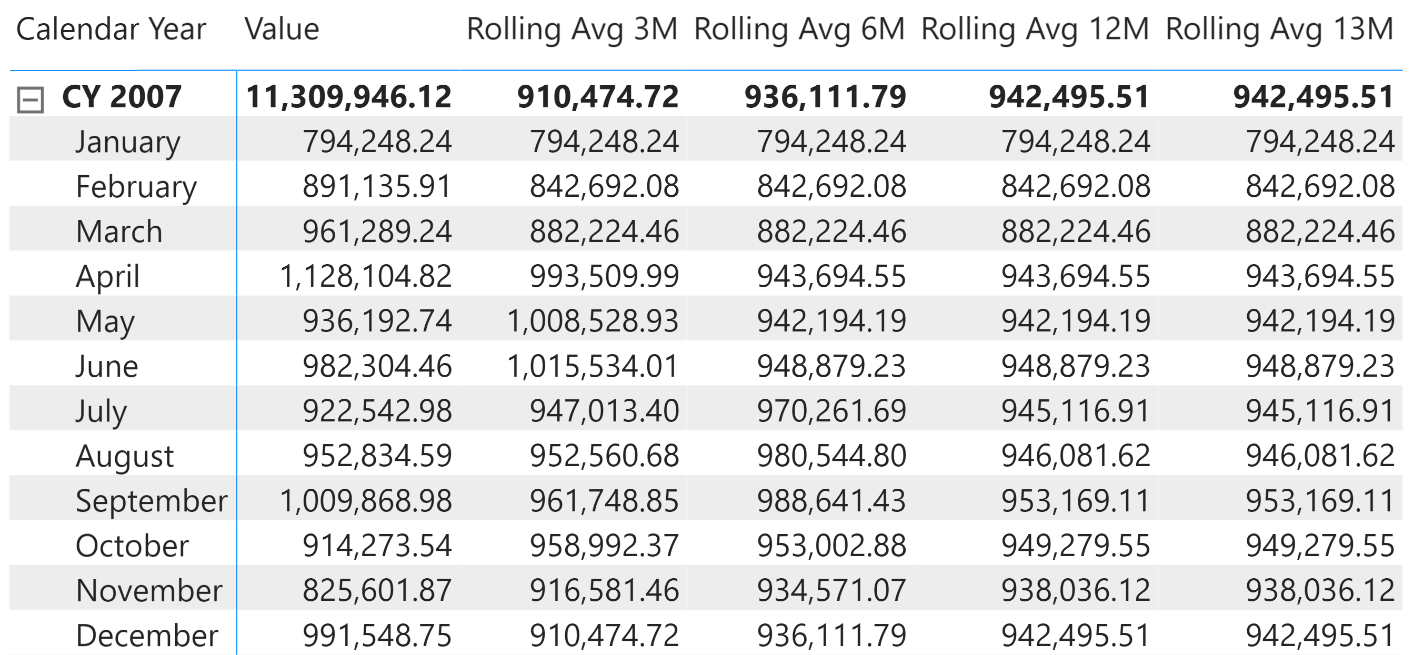
Using the calculation group you can transform any measure into a rolling average, or show different rolling averages in charts and reports. As an example, the following is a matrix showing different rolling averages of sales amount, along with the original sales values.
Conclusion
A rolling average is a very common calculation. It is also known as a moving average or a running average, and it requires you to take into account a time period larger than the one selected in the report.
The DATESINPERIOD function is a simple way to obtain the extended period you need for the moving average. By using DATESINPERIOD, you can change the filter context to retrieve the desired set of dates. DATESINPERIOD works just fine when the desired period for the average is expressed in one of the units of measure it supports, such as days, months, quarters or years. Because DATESINPERIOD always works at the day level, you might find optimized calculations based on months in Month-related calculations on the DAX Patterns website.
If you need to compute a moving average over a given number of weeks, then you cannot rely on DATESINPERIOD. Instead, you will need to use columns in the Date table and follow the more complex implementation that you can find in the Week-related calculations pattern.
Evaluates an expression in a context modified by filters.
CALCULATE ( <Expression> [, <Filter> [, <Filter> [, … ] ] ] )
Returns the dates from the given period.
DATESINPERIOD ( <Dates>, <StartDate>, <NumberOfIntervals>, <Interval> )
Calculates the average (arithmetic mean) of a set of expressions evaluated over a table.
AVERAGEX ( <Table>, <Expression> )
Returns the measure that is currently being evaluated.
SELECTEDMEASURE ( )
 Alberto Ferrari
Alberto Ferrari