An important metric to consider in optimizing DAX is the cardinality of the data structures iterated by the formula engine. Sometimes the formula engine needs to scan huge datacaches because it cannot leverage the auto-exist logic of DAX. Optimizing these scenarios requires a deep understanding of the DAX engine. This article describes an example of such optimization.
The examples used in this article are not related to specific business problems. We want to focus on the behavior of DAX, not on a specific business problem. Let us start with a sample query:
DEFINE
MEASURE Sales[SimpleSum] = SUM ( Sales[Quantity] )
EVALUATE
{
COUNTROWS (
SUMMARIZECOLUMNS (
'Date'[Date],
Customer[Company Name],
'Product'[Color],
"Test", [SimpleSum]
)
)
}
The result of this query is the number of combinations of date, company, and color with sales transactions. In the demo database we are using, it returns 99,067 combinations scanning the 12 million rows of the Sales table in around 50 milliseconds. Nothing exceptional here – this is the speed expected of Power BI.
Nevertheless, it is important to spend some time analyzing exactly how the DAX engine solves the query. The query plan is extremely simple.
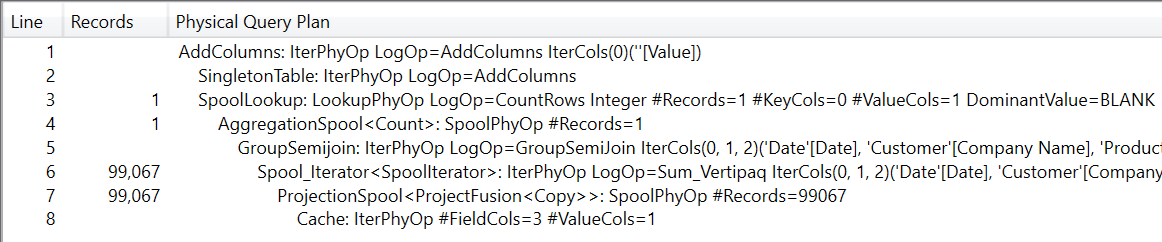
The query plan executes a storage engine (SE) query retrieving the 99,067 combinations from Sales, and then it counts them. Therefore, the SE materializes 99,067 rows scanning Sales. Even though – as humans – we consider this to be a reasonable query plan, the engine performs some complex reasoning to figure out that this is indeed the best way to answer the query. Let us see what happens.
SUMMARIZECOLUMNS requires the engine to group the columns by groups of three, belonging to three different tables. SUMMARIZECOLUMNS also requires the engine to perform the cross-join of the values, and then evaluate the measure. Because the columns belong to different tables, the auto-exist behavior does not kick in (see Understanding DAX auto-exist for more details).
Taken individually, the three columns are not large: Date[Date] contains 2,556 values, Customer[Company Name] contains 386 values and Product[Color] only contains 16 values. However, the full cross-join of these three columns corresponds to the product of the three values. And 2,556*386*16 equals to 15,785,856 possible combinations of values.
Be mindful that – semantically – the query is equivalent to the following one, which shows the required materialization more clearly:
DEFINE
MEASURE Sales[SimpleSum] = SUM ( Sales[Quantity] )
EVALUATE
{
COUNTROWS (
FILTER (
ADDCOLUMNS (
CROSSJOIN (
CROSSJOIN (
VALUES ( 'Date'[Date] ),
VALUES ( Customer[Company Name] )
),
VALUES ( 'Product'[Color] )
),
"Test", [SimpleSum]
),
NOT ( ISBLANK ( [Test] ) )
)
)
}
How does DAX know that it would be useless to scan – and therefore materialize – all the possible combinations, when it can only compute the existing ones instead? The reason is that the measure aggregates the SUM of one column in the Sales table. If Sales does not contain one combination of the three columns, the sum produces no result. Therefore, the optimizer uses this information to produce an optimal query plan, which scans Sales by also joining the other three tables. This way, the scan only retrieves the rows that might produce a result. The following xmSQL query shows the scan executed by the SE:
SELECT
'Customer'[Company Name],
'Date'[Date],
'Product'[Color],
SUM ( 'Sales'[Quantity] )
FROM 'Sales'
LEFT OUTER JOIN 'Customer' ON 'Sales'[CustomerKey] = 'Customer'[CustomerKey]
LEFT OUTER JOIN 'Date' ON 'Sales'[OrderDate] = 'Date'[Date]
LEFT OUTER JOIN 'Product' ON 'Sales'[ProductKey] = 'Product'[ProductKey];
The code executed is equivalent to this DAX query, which is another efficient way to obtain the same result:
DEFINE
MEASURE Sales[SimpleSum] = SUM ( Sales[Quantity] )
EVALUATE
{
COUNTROWS (
ADDCOLUMNS (
SUMMARIZE (
Sales,
'Date'[Date],
Customer[Company Name],
'Product'[Color]
),
"Test", [SimpleSum]
)
)
}
Despite everything being rather simple so far, it is useful to do a first recap:
- The query requires a full cross-join between three dimension tables (Customer, Date, and Product) and it returns the sum of one column from the fact table (Sales).
- The engine checks that the result can be produced if and only if a combination of values from the dimensions does exist in the fact table.
- The optimizer simplifies the query by iterating only the existing combinations; it avoids the scan of 15,000,000 possible combinations, focusing only on the existing 99,000 combinations instead.
In terms of performance, the optimizer does a tremendous job. Indeed, the query containing the explicit CROSSJOIN takes around 8 seconds to run, whereas the optimized version requires a handful of milliseconds.
It is crucial to understand that to apply the optimization, the engine must be sure that the two queries are equivalent.
Slightly changing the query produces very different results. For example, consider the following version where we only changed the measure definition. Instead of computing a sum, the measure now checks if the sum is greater than or equal to zero, returning a Boolean value (TRUE or FALSE):
DEFINE
MEASURE Sales[SimpleBoolean] = SUM ( Sales[Quantity] ) >= 0
EVALUATE
{
COUNTROWS (
SUMMARIZECOLUMNS (
'Date'[Date],
Customer[Company Name],
'Product'[Color],
"Test", [SimpleBoolean]
)
)
}
The result is now 15,785,856. In other words, the engine produces – and evaluates – the full cross-join. The reason is that non-existing combinations of date, company, and color produce a result. The SUM of these non-existing combinations is blank, because there are no sales for non-existing rows. Nevertheless, the combinations are evaluated and the expression result is TRUE for all of the non-existing combinations.
As you might expect, this query is much slower: it runs in around 2 seconds, because it scans over 15,000,000 rows. We strongly suggest you spend some time reading the query plan of this last query.
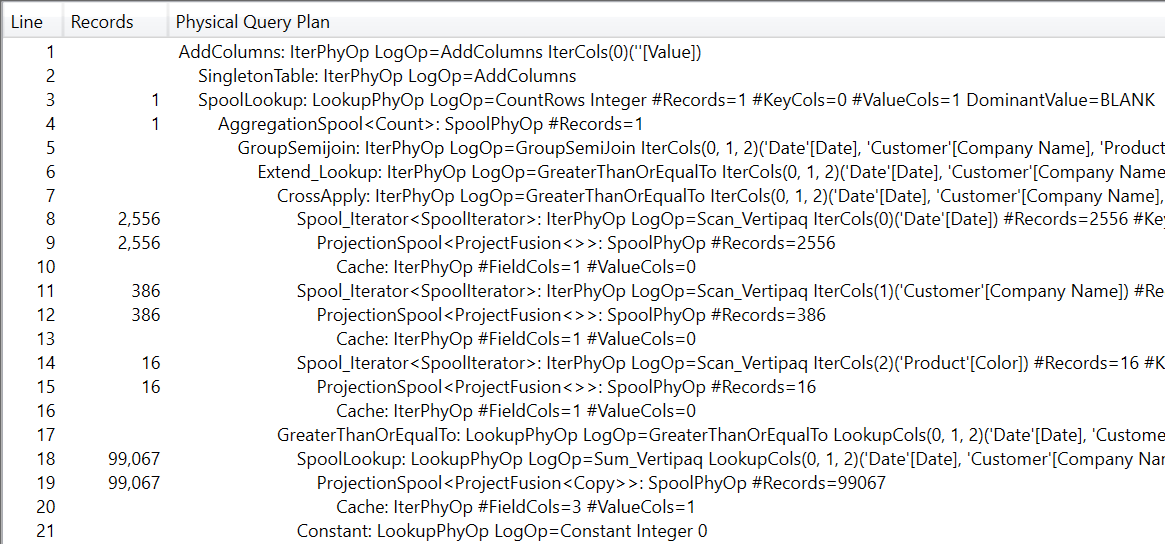
It shows that the optimizer is indeed much better than expected. Instead of computing the measure for all the possible combinations, it computes only the existing combinations in Sales. It then compares the full cross-join of the three columns with the existing combinations in Sales in order to speed up the calculation.
The important detail to remember in this step is that the value of a Boolean condition does not depend on the existence of a combination in the fact table. The Boolean value might be true or false depending on the combination of values from the dimension. In other words, there are 15,000,000 possible values to scan. In this case, the engine does a good job by reducing the number of computations.
It turns out that this is not the slowest query we can analyze in this article. We can further mess with the optimizer and force the production of the worst query plan. The following query generates the slowest query plan:
DEFINE
MEASURE Sales[SimpleIf] =
IF (
SUM ( Sales[Quantity] ) >= 0,
SUM ( Sales[Quantity] )
)
EVALUATE
{
COUNTROWS (
SUMMARIZECOLUMNS (
'Date'[Date],
Customer[Company Name],
'Product'[Color],
"Test", [SimpleIf]
)
)
}
In this query, for each combination of Date, Company Name, and Color, the measure checks if the result is greater than or equal to zero, only summing positive values. The measure serves no purpose other than to demonstrate when the optimizer starts to be confused. Indeed, this query runs in more than 8 seconds, resulting in horrible performance.
At first sight, it looks like the issue is the presence of IF. This is not correct. IF, by itself, is not a big deal. The real issue is the requirement to evaluate non-existing combinations of attributes of the dimensions. IF is useful to spot the problem, but IF by itself is not the only culprit.
The problem with this last query is in the condition that checks if the sum of quantity is greater than or equal to zero. In a DAX comparison, BLANK is considered as zero. Therefore, a measure that evaluates to blank is treated as zero and any non-existing combination of the dimensions satisfies the IF statement. Therefore, the engine must evaluate more than 15,000,000 combinations, requiring a long execution time.
Fixing the code in this scenario is utterly simple. It is enough to tell DAX that we are not interested in zeros – therefore in blanks. If instead of using greater than or equal to (>=) we just check for strictly greater than (>), then blank values are no longer part of the game:
DEFINE
MEASURE Sales[SimpleIf] =
IF (
SUM ( Sales[Quantity] ) > 0,
SUM ( Sales[Quantity] )
)
EVALUATE
{
COUNTROWS (
SUMMARIZECOLUMNS (
'Date'[Date],
Customer[Company Name],
'Product'[Color],
"Test", [SimpleIf]
)
)
}
This last query restores the great performance of DAX, evaluating only the relevant rows.
In the example used for these demos, excluding the zero value from the condition solved the issue. More generally, adding a bit of code to explicitly remove blank values from the calculation greatly helps the optimizer find the best path. For example, the following formulation – though more verbose – runs nearly as fast as the latter one:
DEFINE
MEASURE Sales[SimpleIf] =
IF (
NOT ISBLANK ( SUM ( Sales[Quantity] ) ),
IF (
SUM ( Sales[Quantity] ) > 0,
SUM ( Sales[Quantity] )
)
)
EVALUATE
{
COUNTROWS (
SUMMARIZECOLUMNS (
'Date'[Date],
Customer[Company Name],
'Product'[Color],
"Test", [SimpleIf]
)
)
}
The code may look more complex, but providing the required information to the engine on how to treat blanks produces a tangible and efficient result.
Finally, it is worth noting that similar results can be obtained by using variables. Variables greatly help the optimizer understand the code we author, producing optimal paths in the execution plan. This last version of the query is the fastest among all the different versions analyzed:
DEFINE
MEASURE Sales[SimpleIf] =
VAR S = SUM ( Sales[Quantity] )
RETURN IF ( S >= 0, S )
EVALUATE
{
COUNTROWS (
SUMMARIZECOLUMNS (
'Date'[Date],
Customer[Company Name],
'Product'[Color],
"Test", [SimpleIf]
)
)
}
Understanding the reason why a variable solves the problem is a bit more intricate. By using a variable, we are telling the optimizer that we want to aggregate all the rows using SUM, regardless of whether the condition in the IF function is met or not. This turns on eager evaluation for the measure – a that is, the values are computed in block and then the IF condition is used to add only the positive results. The eager computation of the sum of Sales[Quantity] produces only 99,000 values, making it possible to generate an efficient query plan. Describing it further takes an article of its own: you can read Understanding eager vs. string evaluation in DAX to know more about it.
As it always goes with articles about DAX optimization, we do not want to share any golden rule, mainly because we genuinely know there are none. Nevertheless, when optimizing your code always pay attention to the number of rows iterated by the formula engine. Large iterations are often generated by an inaccurate treatment of blanks, which are often present because of non-existing combinations of dimensions that the engine must iterate to guarantee the equivalence between BLANK and zero.
Create a summary table for the requested totals over set of groups.
SUMMARIZECOLUMNS ( [<GroupBy_ColumnName> [, [<FilterTable>] [, [<Name>] [, [<Expression>] [, <GroupBy_ColumnName> [, [<FilterTable>] [, [<Name>] [, [<Expression>] [, … ] ] ] ] ] ] ] ] ] )
Adds all the numbers in a column.
SUM ( <ColumnName> )
Returns a table that is a crossjoin of the specified tables.
CROSSJOIN ( <Table> [, <Table> [, … ] ] )
Checks whether a condition is met, and returns one value if TRUE, and another value if FALSE.
IF ( <LogicalTest>, <ResultIfTrue> [, <ResultIfFalse>] )
Returns a blank.
BLANK ( )
 Marco Russo & Alberto Ferrari
Marco Russo & Alberto Ferrari